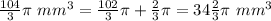Question

1. Define the shapes that make up the figure.

2. Identify the volume formula(s) that will be be used for each shape in number 1.
3. Find the volume for each individual shape.
4. Find the composite volume of the original figure.

Answer 1

Part 1) The shapes that make up the figure are two hemispheres and a cylinder

Part 2) see the explanation

Part 3) see the explanation

Part 4)
`V=34(2)/(3)\pi\ mm^3`

Explanation:

Part 1) Define the shapes that make up the figure.

we know that

The shapes that make up the figure are two hemispheres and a horizontal cylinder

Part 2) Identify the volume formula(s) that will be be used for each shape in number 1.

we know that

The volume of a hemisphere is equal to

`V=(2)/(3)\pi r^(3)`

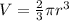
where

r is the radius of the hemisphere

The volume of a cylinder is equal to

`V=\pi r^(2)h`

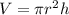
where

r is the radius of the base of cylinder

h is the height or length of the cylinder

Part 3) Find the volume for each individual shape.

step 1

Find the volume of a hemisphere

`V=(2)/(3)\pi r^(3)`

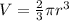
we have

`r=2\ mm`

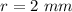
substitute

`V=(2)/(3)\pi (2)^(3)`

`V=(16)/(3)\pi\ mm^(3)`

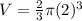
step 2

Find the volume of the horizontal cylinder

`V=\pi r^(2)h`

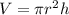
we have

`r=2\ mm`

`h=10-2-2=6\ mm`

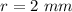
substitute

`V=\pi (2)^(2)(6)`

`V=24\pi\ mm^3`

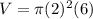
Part 4) Find the composite volume of the original figure

The volume of the composite figure is equal to the volume of two hemisphere plus the volume of the cylinder

so

`V=2((16)/(3)\pi)+24\pi\\\\V=(32)/(3)\pi+24\pi`

`V=(104)/(3)\pi\ mm^3`

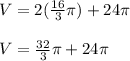
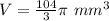
Convert to mixed number

`(104)/(3)\pi\ mm^3=(102)/(3)\pi+(2)/(3)\pi=34(2)/(3)\pi\ mm^3`