Answer:
a) The employer can fill the four positions in 495 ways.
b) The employer can fill the four positions in 210 ways.
Step-by-step explanation:
The order is not important.
For example:
Selecting John, Laura, Mary and Tre'Davious is the same as selecting Laura, John, Mary and Tre'Davious.
So we use the combinations formula to solve this problem.
Combinations formula:
 is the number of different combinations of x objects from a set of n elements, given by the following formula.
is the number of different combinations of x objects from a set of n elements, given by the following formula.

(a) the selection is random
There are 12 people, and 4 are selected. So
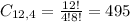
(b) exactly two selections are women?
There are 7 men and 5 women. We want to select 2 men and 2 women. So
