To solve this problem we will apply the concept of potential difference defined as the product between the electric field and distance, that is
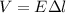
Here,
E = Electric Field
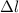 = Length
= Length
Our values are,
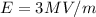
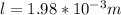
Replacing,
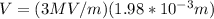

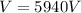
Therefore the difference potential between you and your friend just before the spark is 5940V