Question

Factor the polynomial completely.

Answer 1

The factors of the polynomial: (b⁴ - 2)(b² - 3)

Explanation:

The given polynomial is:
`$ \textbf{b}^{\textbf{6}} \textbf{-3b}^{\textbf{4}} \textbf{-2b}^{\textbf{2}} \textbf{+ 6} $`

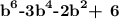
We can factor the given polynomial by grouping.

We get:
`$ \{ b^6 - 3b^4\} + \{2b^2 + 6\} $`

`$ = b^4 (b^2 - 3) -2(b^2 - 3) $`

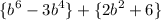
Taking (b² - 3) common outside, we get:

`$ = \{b^2 - 3\} \{b^4 - 2\} $`

Hence the polynomial
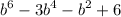`$ b^6 - 3b^4 - b^2 + 6 $` can be factored as
`$ (b^4 - 2)(b^2 - 3) $`.

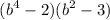Hence, the answer.