Question

A boat can travel 12 km down the river in the same time it can go 4 km up the river. If the current in the river is 2 km per hour, how fast can the boat travel in still water?

I know the answer is "4 km per hour" from the book but I don't know how to show the work so please help me. thank you

Answer 1

The speed of the boat in still water is 4 km per hour

Explanation:

Let

s ---> the total speed of the boat in km/h

x ----> the speed of the boat in still water in km/h

t ----> the time in hours

d ---> the distance in km

Remember that the speed is equal to the distance divided by the time

so

The time is the distance divided by the speed

so

Down the river

`t=(d)/(s)`

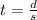
we have

`d=12\ km\\s=(x+2)\ km/h`

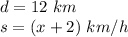
Remember that the speed of the boat down the river is equal to the speed of the boat in still water plus the speed of the current

substitute

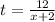`t=(12)/(x+2)` ----> equation A

Up the river

`t=(d)/(s)`

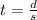
we have

`d=4\ km\\s=(x-2)\ km/h`

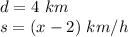
Remember that the speed of the boat up the river is equal to the speed of the boat in still water minus the speed of the current

substitute

`t=(4)/(x-2)` ----> equation B

Equate equation A and equation B

`(12)/(x+2)=(4)/(x-2)`

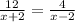
solve for x

Multiply in cross

`12(x-2)=4(x+2)\\12x-24=4x+8\\12x-4x=24+8\\8x=32\\x=4\ km/h`

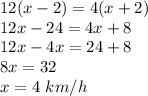
therefore

The speed of the boat in still water is 4 km per hour