Question

Arithmetic average of real nonnegative numbers is always smaller than or equal to geometric average. Group of answer choices True False

Answer 1

False

Explanation:

Actually, the arithmetic average (or mean) is always greater or equal than the geometric average. This is known as the Arithmetic-Geometric inequality (AM inequality). Let a,b be two real numbers, then the AM inequality states that

`(a+b)/(2)\geq √(ab)`

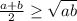
To see that the given statement is false, consider a=1, b=3. The arithmetic mean is equal to (1+3)/2=2, and the geometric mean is equal to
`√(1\cdot 3)=√(3)` but
`2>√(3)`, contrary to the statement (arithmetic>geometric in this case).