Question

A person on the ground looks up at an angle of 28° and sees the top of a tree and the top of a building aligned. The tree is 20 m away from the person and the building is 60 m away from the person. What is the difference in heights between the building and tree?

Answer 1

21.27 meters.

Explanation:

Please find the attachment.

Let H and h represent height of building and tree respectively.

We have been given that a person on the ground looks up at an angle of 28° and sees the top of a tree and the top of a building aligned. The tree is 20 m away from the person and the building is 60 m away from the person.

We know that tangent relates opposite side of a right triangle with its adjacent side.

`\text{tan}=\frac{\text{Opposite}}{\text{Adjacent}}`

`\text{tan}(28^(\circ))=(H)/(60)`

`60\cdot \text{tan}(28^(\circ))=H`

`60\cdot 0.531709431661=H`

`H=31.90256589966\approx 31.90`

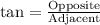
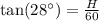
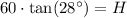
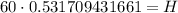
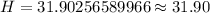
Similarly, we can find height of the tree.

`\text{tan}(28^(\circ))=(h)/(20)`

`20\cdot\text{tan}(28^(\circ))=h`

`20\cdot 0.531709431661=h`

`h=10.63418863322\approx 10.63`

`H-h=31.90-10.63`

`H-h=21.27`

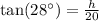
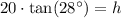
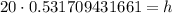
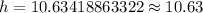
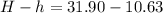
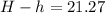
Therefore, the difference in heights between the building and tree is 21.27 meters.