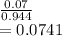Question

A machine produces defective parts with three different probabilities depending on its state of repair. If the machine is in good working order, it produces defective parts with probability 0.02. If it is wearing down, it produces defective parts with probaly 0.1. If it needs maintenance, it produces defective parts with probability 0.3. The probability that the machine is in good working order is 0.8; the probability that it is wearing down is 0.1; and the probability that it needs maintenance is 0.1

(a) Given a good working machine, compute the probability that one of its randomly selected parts will be defective.
(b) Compute the probability that a randomly selected part will be defective.
(c) Suppose a randomly selected part is not defective. Compute the probability that it comes from a machine that needs maintenance.

Answer 1

Explanation:

Given that a machine produces defective parts with three different probabilities depending on its state of repair.

condition Good order Wearing down Needs main Total

Prob 0.8 0.1 0.1 1

Defective 0.02 0.1 0.3

Joint prob 0.016 0.01 0.03 0.056

a) 0.016

b) total = 0.056

c) If not defective from needs maintenance

Prob for not defective =
`0.8*0.98+0.1*0.9+0.1*0.7\\=0.784+0.09+0.07\\=0.944`

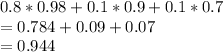
From machine that needs maintenance = 0.07

So reqd prob =
`(0.07)/(0.944) \\=0.0741`