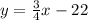Question

what is the equation of the line that is parallel to 6x-2y=4+6y and passes through the point (8, -16)?

Answer 1

`y=(3)/(4)x-22`

Explanation:

We are given;

• The equation of a line 6x-2y=4+6y
• A point (8, -16)

We are required to determine the equation of a line parallel to the given line and passing through the given point.

• One way we can determine the equation of a line is when we are given its slope and a point where it is passing through,

First we get the slope of the line from the equation given;

• We write the equation in the form y = mx + c, where m is the slope

That is;

6x-2y=4+6y

6y + 2y = 6x-4

8y = 6x -4

We get, y = 3/4 x - 4

Therefore, the slope, m₁ = 3/4

But; for parallel lines m₁=m₂

Therefore, the slope of the line in question, m₂ = 3/4

To get the equation of the line;

We take a point (x, y) and the point (8, -16) together with the slope;

That is;

`((y--16)/(x-8)=(3)/(4)`

`4(y+16)=3(x-8)\\4y + 64 = 3x - 24\\4y=3x-88\\ y=(3)/(4)x-22`

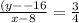
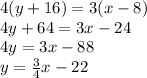
Thus, the equation required is
`y=(3)/(4)x-22`