Question

A die with six faces has the number 1 painted on three of its faces, the number 2 painted on 2 of its faces, and number 3 on one face. Assume each face is equally likely to come up.

a) Find a sample space.
b) Find P(odd number).
c) If die were loaded so that the face with 3 on it were twice as likely to come up as the other 5 faces, would this change the sample space?
d) If die were loaded so that the face with 3 on it were twice as likely to come up as the other 5 faces, would this change the value of P(odd number)?

Answer 1

a) S = {1, 2, 3}

b) P(odd number) =
`(2)/(3)`

c) No

d) Yes

Explanation:

a) The sample space is the set of all possible outcomes. By definition, the elements of a set should not be repeated. Hence, the sample space S = {1, 2, 3}

However, the sample is not equiprobable because each element has different probabilities.

b) P(odd number) =
`(number of odd digits)/(number of faces)=(4)/(6)=(2)/(3)`

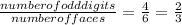
Note that the odd numbers are 1 (on three faces) and 3 (on one face).

c) The fact the die has been biased does not change the possible outcomes. It only changes the probability of getting any given number.

d) Because the 3-face has been loaded, this probability changes. In fact, it is calculated thus:

Let's assume the probability for 1 or 2 is
`x`. Then that of 3 is
`2x`(because it is twice the others). The sum of probabilities must be 1.

`x+x+x+x+x+2x=1`

`7x=1`

`x=(1)/(7)`

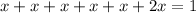
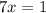
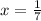
P(odd number) =
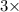`3*`Prob(1) + Prob(3)

=
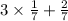`3*(1)/(7)+(2)/(7)` =
`(5)/(7)`