Answer:

Explanation:
Given that set A={1,2,3,...,n},
and set X be the collection of all the functions from A to A.
From A to A functions should be such that each element in A has a unique image in A
Each element has n choices to select the image
So total number of functions from A to A=
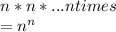
If injective if one element in A is selected as image it should not be image for other element
So first element has n ways, second n-1 ways and so on
No .of injective functions =
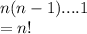
So probability for injective funcitons
=
