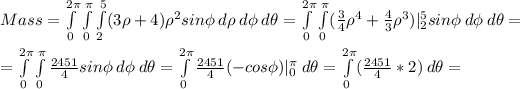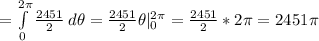Answer:
a)
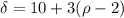
b)
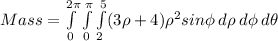
c)
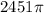
Explanation:
We will use spherical coordinates.
Since δ = 10 and ρ = 2 for inner and δ=16 and ρ = 5 for outer, the density increases at a rate of 3 g/cm^3 for each cm increase in radius.
a) Hence, the equation of density (δ) as a function of radius (ρ) is as follows:
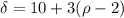
b) The equation to find Mass can be written with triple integration as follows:
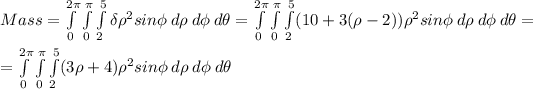
c) Now, we will calculate the integral above as follows: