Question

A bicyclist is finishing his repair of a flat tire when a friend rides by with a constant speed of 3.63 m/s. Four seconds later, the bicyclist hops on his bike and accelerates at 2.11 m/s2 until he catches his friend. How much time does it take until he catches his friend?

Answer 1

t = 5.81 s,

Step-by-step explanation:

given,

constant speed of friend, v = 3.63 m/s

time = 4 s

acceleration of the cyclist = 2.11 m/s²

time taken by the cyclist to meet his friend.

distance by his friend in 4 s

d = 3.63 x 4

d = 14.52 m

To meet his friend distance travel by the by cyclist is should be same as his friend.

distance travel by cyclist in t sec.

`D = u t + (1)/(2)at^2`

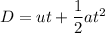
initial velocity is zero

`D =  (1)/(2)* 2.11 * t^2`......()

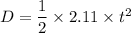distance travel in t second by hid friend

D = 14.52 + 3.63 t

equating both equation (1) and (2)

`(1)/(2)* 2.11 * t^2 = 14.52 + 3.63 t`

`1.055 t^2 - 3.63 t - 14.52 = 0`

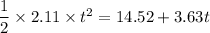
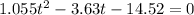
on solving quadratic equation

t = 5.81 s, -2.36 s

hence, time taken to catch his friend is equal to 5.81 s