Question

Considering the number of questions incorrect from classmates on a quiz {10, 11, 12, 13, 13, 13, 14, 15, 16, 16, 17, 18, 18, 19, 20}. According to the Empirical Rule, 68% of the data should fall between what two numbers?

Answer 1

According to the Empirical Rule, 68% of the data should fall between 11.98 and 18.02

Explanation:

We are given the following data in the question:

10, 11, 12, 13, 13, 13, 14, 15, 16, 16, 17, 18, 18, 19, 20

Formula:

`\text{Standard Deviation} = \sqrt{\displaystyle\frac{\sum (x_i -\bar{x})^2}{n-1}}`

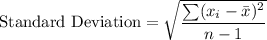
where
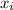`x_i` are data points,
`\bar{x}` is the mean and n is the number of observations.

`Mean = \displaystyle\frac{\text{Sum of all observations}}{\text{Total number of observation}}`

`Mean =\displaystyle(225)/(15) = 15`

Sum of squares of differences = 25 + 16 + 9 + 4 + 4+ 4 + 1 + 0+ 1+ 1 + 4 + 9 + 9+ 16 + 25 = 128

`S.D = \sqrt{(128)/(14)} = 3.02`

Empirical rule:

• According to this rule almost all the data lies within three standard deviation of the mean for a normal distribution.
• About 68% of data lies within one standard deviation of the mean.
• About 95% of data lies within two standard deviations of mean.
• Arround 99.7% of data lies within three standard deviation of mean.

Thus, by empirical rule,

`\mu \pm 1\sigma = 15\pm (3.02) = (11.98,18.02)`

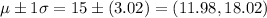
According to the Empirical Rule, 68% of the data should fall between 11.98 and 18.02