Answer:
$550
Explanation:
The 1.7th percentile of a normal distribution has a corresponding z-score of -2.12
For any given value of monthly earnings, X, the z-score is defined as:
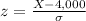
For z=-2.12, and X = 2,834, the standard deviation is:

The standard deviation of the monthly earnings of the computer programmers is $550.