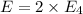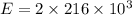Question

Three +3.0-μC point charges are at the three corners of a square of side 0.50 m. The last corner is occupied by a −3.0-μC charge. Find the magnitude of the electric field at the center of the square. (k=1/4πϵ0=8.99×109 N.m^2/C^2)

Answer 1

E = 440816.32 N/C

Step-by-step explanation:

Given data:

Three point charge of charge equal to +3.0 micro coulomb

fourth point charge = - 3.0 micro coulomb

side of square = 0.50 m

`K =1/4 \pi \epsilon_0 = 8.99 * 10^9` N.m^2/c^2

Due to having equal charge on center of square, 2 charge produce equal electric field at center and other two also produce electric field at center of same value

So we have

`E_1 + E_3 = 0`

`E =E_2 + E_4`

`E = 2 E_2`

[
`E_2 =(2* k * q)/(r^2)`

[
`r= ((0.5^2 + 0.5^2)^2)/(2) = 0.35 m`]

plugging all value

`E = 2 E_2`

`E = 2 E_2 =(2* k * q)/(r^2)`

`E = (2 * 8.99 * 10^93* 10^(-6))/(0.35^2)`

E = 440816.32 N/C

Answer 2

`E=4.32* 10^(5)\ N.C^(-1)`

Step-by-step explanation:

Given:

• charges at the each of the three corner of a square,
  `q_1=q_2=q_3=+3* 10^(-6)\ C`

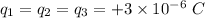
• side of the square,
  `a=0.5\ m`

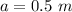
• charge at the remaining corner of the square,
  `q_4=-3* 10^(-6)\ C`

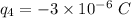
Distance of the center of the square from each of the vertex of square:

Using Pythagoras theorem:

`d^2+d^2=a^2`

`2d^2=0.5^2`

`d=0.3536\ m`

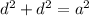
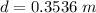
As there two equal like charges at an equal distance on the opposite ends of a diagonal so they will cancel out the effect of field due to each other.

Electric field at the center of the square due to
`q_4`:

`E_4=(1)/(4\pi.\epsilon_0) * (q_4)/(d^2)`

`E_4=9* 10^9*(3* 10^(-6))/(0.125)`

`E_4=216*10^(3)\ N.C^(-1)`

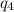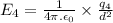
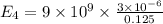
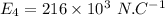
The charge on the opposite vertex will have the equal effect in the same direction which is towards the charge
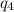`q_4`. (refer the attached schematic)

So, the net electric field at the center:

`E=2* E_4`

`E=2* 216* 10^3`

`E=4.32* 10^(5)\ N.C^(-1)`