Question

A spotlight on the ground shines on a wall 12 meters away. If a man 2 meters tall walks from the spotlight toward the building at a speed of 1.6 m/s, how fast is the length of his shadow on the building decreasing when he is 4 meters from the building?

Answer 1

Height of shadow decreasing at rate of of -0.6 m/s

Explanation:

Consider the figure attached below.

Height of man = 2 m

Height of shadow = y

Distance between spot light and wall = 12 m

To find:

Rate of decrease i shadow when man is 4 m away from wall

Form figure (2), there are two right angle triangles in figure (1) sharing the common angles

From trigonometry for two right angle triangles sharing the common angles, ratio of adjacent side length to opposite side length is equal. i.e

`(adjacent\,side\,length)/(opposite\,side\,length)=(x)/(2)=(12)/(y)\\\\xy=24--(1)\\`

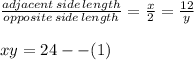
When man is 4 m away from wall height of shadow is

x+4 =12

x = 8 m

Then

(8)(y)=24

y = 3 m

Speed of man = dx/dt = 1.6 m/s

Differentiating (1) w.r.to 't'

`(d)/(dt)(xy)= (d)/(dt)24\\\\y.(dx)/(dt)+x.(dy)/(dt)=0\\\\Using\\y=3\,,\,x=8\,,\,(dx)/(dt)=1.6\\\\(3)(1.6)+8(dy)/(dt)=0\\\\(dy)/(dt)=-0.6\,ms^(-1)`

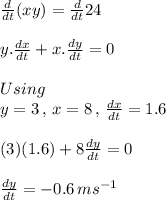
Negative sign shows the decrease in length of shadow.