Question

semi anThe bones of a prehistoric man found in the desert of New Mexico contain approximately 5% of the original amount of carbon 14. If the half-life of carbon 14 is 5700 years, approximately how long ago did the man die?

Answer 1

24555 years

Step-by-step explanation:

Data provided in the question:

Half life of carbon 14 = 5700 years

carbon present in the dead man = 5% of the original amount of carbon 14

Now,

let the initial Amount of carbon be 'A'

Therefore,

after half life

Amount of carbon =
`(A)/(2)`

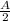
Thus,

`(A)/(2)` =
`Ae^(kt)`

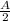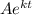
here,

k is the decay constant

t is the time = 5700 years

therefore,

1 =
`2e^(k*5700)`

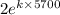
or

0.5 =
`e^(k*5700)`

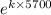
taking natural log both the sides

-0.69314 = 5700k

or

k = - 0.000122

therefore,

for dead man Amount of carbon = 5% of A = 0.05A

thus,

0.05A =
`Ae^(( - 0.000122)t)`

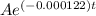
or

0.05 =
`e^(( - 0.000122)t)`

taking natural log both the sides

we get

-2.995 = - 0.000122 × t

or

t = 24555.18 ≈ 24555 years