Question

Estimate the instantaneous rate of change of P ( x ) = 3 x 2 + 5 at the point x = − 2 In other words, choose x-values that are getting closer and closer to − 2 and compute the slope of the secant lines at each value. Then, use the trend/pattern you see to estimate the slope of the tangent line.

Answer 1

The slope of the tangent line is -12

Explanation:

Instantaneous Rate of Change

We can approximate to the value of the slope of one function P(x) by computing the slope of the secant line as follows

`\displaystyle m=(P(x+\Delta x)-P(x))/(\Delta x)`

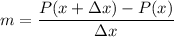
Where
`\Delta x` is an infinitesimal change of x, as small as we want. Our function is

`\displaystyle P(x)=3x^2+5`

We are required to find the instantaneous rate of change in x=-2 by iteratively getting close to it and estimating the slope according to the observed trend.

Let´s use

`\displaystyle \Delta x=0.1`

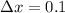
Then the approximate slope of P in x=-2 is

`\displaystyle m=(P(-2+0.1)-P(-2))/(0.1)`

`\displaystyle m=(P(-1.9)-P(-2))/(0.1)`

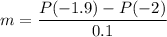
We compute

`\displaystyle P(-1.9)=3(-1.9)^2+5=15.84`

`\displaystyle P(-2)=3(-2)^2+5=17`

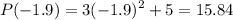
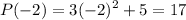
Replacing in the slope

`\displaystyle m=(15.83-17)/(0.1)=-11.7`

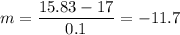
Now we use a smaller infinitesimal or differential

`\displaystyle \Delta x=0.01`

`\displaystyle m=(P(-2+0.01)-P(-2))/(0.01)`

`\displaystyle m=(P(-1.99)-P(-2))/(0.01)`

`\displaystyle P(-1.99)=3(-1.99)^2+5=16.88`

`\displaystyle m=(16.88-17)/(0.01)=-11.97`

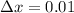
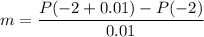
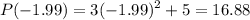
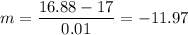
We can see the slope is getting closer to -12 as the infinitesimal tends to 0, thus we can estimate the slope of the tangent line is -12