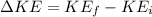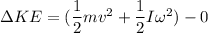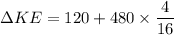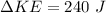Answer
given,
radius of merry - go - round = 4 m
mass of the disk = 120 kg
speed of the merry- go-round = 0 rad/s
speed = 2 m/s
mass of student = 60 kg

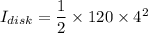
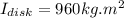
initial angular momentum of the system
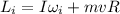
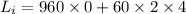
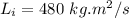
final angular momentum of the system
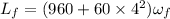
from conservation of angular momentum


now,
change in kinetic energy of the system
initially the merry-go-round was on rest KE_i = 0