Question

A clamped 24 cm wire with 25 g/m mass density vibrates at its fundamental mode near an 85 cm long open/closed tube. The wire vibration excites the second harmonic of the tube. What is the tension in the wire in N?

Answer 1

T = 518.4 N

Step-by-step explanation:

Length of wire,l = 24 cm = 0.24 m

mass density of wire,μ = 25 g/m = 0.025 g/m

Length of the tube, L = 85 cm = 0.85 m

speed of sound, v = 340 m/s

frequency in the tube in open/closed tube

`f_(3) = (3v)/(4L)`

`f_(3) = (3* 340)/(4* 0.85)`

`f_(3) = 300\ Hz`

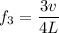
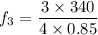
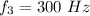
now, calculation of tension in the wire.

Frequency in the wire will be same as frequency in the tube

`f = (v_(wire))/(2 l)`

`v_(wire) = \sqrt{(T)/(\mu)}`

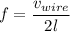
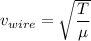
now,

`f = (1)/(2 l)* \sqrt{(T)/(\mu)}`

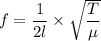
squaring both side and arranging

`T = f^2* 4l^2 * \mu`

`T = 300^2* 4* 0.24^2 * 0.025`

T = 518.4 N

hence, the tension in wire is equal to T = 518.4 N