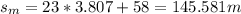Question

A motorcycle is following a car that is traveling at a constant speed on a straight highway. Initially, the car and the motorcycle are both traveling at the same speed of 23.0 m/s, and the distance between them is 58.0 m. After t1 = 5.00 s, the motorcycle starts to accelerate at a rate of 8.00 m/s^2.

(a) The motorcycle catches up with the car at some time t2. How long does it take from the moment when the motorcycle starts to accelerate until it catches up with the car? In other words, find t2−t1.
(b) How far does the motorcycle travel from the moment it starts to accelerate (at time t1) until it catches up with the car (at time t2)? Should you need to use an answer from a previous part, make sure you use the unrounded value.

Answer 1

(a) 3.807 s

(b) 145.581 m

Step-by-step explanation:

Let Δt = t2 - t1 be the time it takes from the moment when the motorcycle starts to accelerate until it catches up with the car. We know that before the acceleration, both vehicles are travelling at a constant speed. So they would maintain a distance of 58 m prior to the acceleration.

The distance traveled by car after Δt (seconds) at
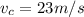`v_c = 23m/s` speed is

`s_c = \Delta t v_c = 23\Delta t`

The distance traveled by the motorcycle after Δt (seconds) at
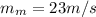`m_m = 23 m/s` speed and acceleration of a = 8 m/s2 is

`s_m = \Delta t v_m + a\Delta t^2/2`

`s_m = 23\Delta t + 8\Delta t^2/2 = 23 \Delta t + 4 \Delta t^2`

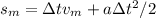
We know that the motorcycle catches up to the car after Δt, so it must have covered the distance that the car travels, plus their initial distance:

`s_m = s_c + 58`

`23 \Delta t + 4 \Delta t^2 = 23\Delta t + 58`

`4 \Delta t^2 = 58`

`\Delta t^2 = 14.5`

`\Delta t = √(14.5) = 3.807s`

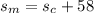
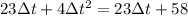
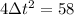
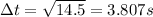
(b)

`s_m = 23 \Delta t + 4 \Delta t^2`

`s_m = 23*3.807 + 58 = 145.581 m`