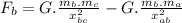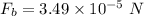Answer:
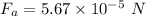
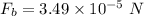
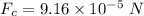
Step-by-step explanation:
Given:
- mass of particle A,
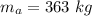
- mass of particle B,
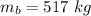
- mass of particle C,
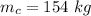
- All the three particles lie on a straight line.
- Distance between particle A and B,

- Distance between particle B and C,
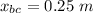
Since the gravitational force is attractive in nature it will add up when enacted from the same direction.
Force on particle A due to particles B & C:

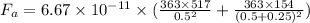
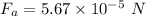
Force on particle C due to particles B & A:
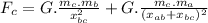
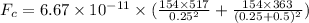
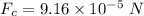
Force on particle B due to particles C & A: