Question

A buffer solution is composed of 1.00 mol of acid and 2.25 mol of the conjugate base. If the p K a of the acid is 4.90 , what is the pH of the buffer?

Answer 1

Answer: The pH of the buffer is 5.25

Step-by-step explanation:

Let the volume of buffer solution be V

We know that:

`\text{Molarity}=\frac{\text{Moles of solute}}{\text{Volume of solution}}`

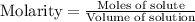
To calculate the pH of acidic buffer, we use the equation given by Henderson Hasselbalch:

`pH=pK_a+\log(\frac{[\text{conjugate base}]}{[acid]})`

We are given:

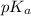`pK_a` = negative logarithm of acid dissociation constant of weak acid = 4.90

`[\text{conjugate base}]=(2.25)/(V)`

`[acid]=(1.00)/(V)`

pH = ?

Putting values in above equation, we get:

`pH=4.90+\log((2.25/V)/(1.00/V))\\\\pH=5.25`

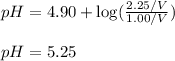
Hence, the pH of the buffer is 5.25