Answer:
four numbers are 1, 3, 5, 7
Explanation:
The sum of four numbers in arithmetic progression is 16
a, a+d, a+2d, a+3d are the four arithmetic series
sum of 4 numbers are

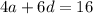
divide both sides by 2
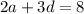
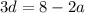
The square of the last number is the square of the first number plus 48.
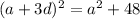
solve for a and d
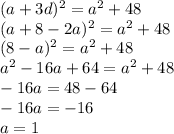
Now find out 'd'
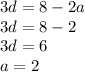
a, a+d, a+2d, a+3d
four numbers are 1, 3, 5, 7