Question

Determine the approximate value of x.

a. 2.045
b.3.264
c.6.736
d.not enough information

Answer 1

Option (C) 6.736

Explanation:

Please look at the attached modified schematic, where I have constructed a perpendicular line to the base of the triangle.

This creates two Right triangles (i.e. one angle will always be 90°). In doing so, the 80° angle is divided into 30° and 50° angles. In doing so we also then know that on the left Right-triangle the bottom left angle will be 60° since for any Triangle all three angles must add up to 180°.

(Check your self: On the left triangle we have 90° + 30° + 60° = 180° and on the right triangle we have 90° + 50° + 40° = 180°, so we are correct).

Now let us first find the value of side named
`y` on the figure using Right-triangle Trigonometry. In a Right-triangle the longest side is called the hypotenuse (here denoted by the sides
`x` and the one valued
`5`).

So we have:

`sin(60)=(opposite side)/(hypotenuse)= (y)/(5)\\`

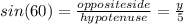
so solving for
`y` gives:

`sin(60)=(y)/(5)\\ y=5sin(60)\\y=(5√(3) )/(2)`

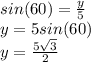
Similarly for the other triangle we can write:

`sin(40)=(y)/(x)\\\\`

`sin(40)=((5√(3) )/(2) )/(x)\\`

`x=((5√(3) )/(2) )/(sin(40))\\\\x=6.736`

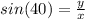
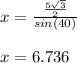
So the correct option is Option (C) 6.736