Question

The sound source of a ship’s sonar system operates at a frequency of 22.0 kHz . The speed of sound in water (assumed to be at a uniform 20∘C) is 1482 m/s . What is the difference in frequency between the directly radiated waves and the waves reflected from a whale traveling straight toward the ship at 4.95 m/s ? Assume that the ship is at rest in the water.

Your target variable is Δf, the magnitude of the difference in frequency between the waves emitted from the sonar device and the waves received by the device after reflecting off the whale. Write an expression for Δf in terms of the relevant frequencies using the subscript notation introduced above.

Express your answer in terms of some or all of the variables fLe, fLr, fSe, and fSr.

Δf =

Answer 1

`\Delta f=f_(Lr)-f_(Se)`

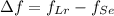
147.45 Hz

Step-by-step explanation:

v = Speed of sound in water = 1482 m/s

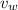`v_w` = Speed of whale = 4.95 m/s

Frequency of the wave in stationary condition

`f_(Lr)=f(v+v_w)/(v-v_w)`

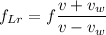
Ship's frequency which is reflected back

`f_(Se)=f(v)/(v-v_w)`

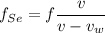
The difference in frequency is given by

`\Delta f=f(v+v_w)/(v-v_w)-f(v)/(v-v_w)\\\Rightarrow \Delta f=f_(Lr)-f_(Se)`

`\mathbf{\Delta f=f_(Lr)-f_(Se)}`

`f_(Lr)=22* (1482+4.95)/(1482-4.95)\\\Rightarrow f_(Lr)=22.14745\ kHz`

`f_(Se)=22\ kHz`

`\Delta f=f_(Lr)-f_(Se)\\\Rightarrow \Delta f=22.14745-22\\\Rightarrow \Delta f=0.14745\ kHz\\\Rightarrow \Delta f=147.45\ Hz`

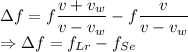
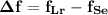
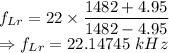
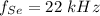
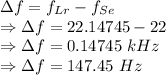
The difference in wavelength is 147.45 Hz