Question

The length of a snake in a video game doubles every minute. The function f(x) = 10. (2)* represents

the length of the snake in centimeters (cm). The time x = 0 represents when the game started.

Answer 1

Part a) see the explanation

Part b) The graph in the attached figure

Explanation:

The complete question is

The length of a snake in a video game doubles every minute. the function f(x)=10*(2)^x represents the length of the snake in centimeters. the time x=0 represents when the game started.

a) label the correct axes with "length (cm)" and"time (minutes)"

b) graph f(x)=10*(2)^x

Part a) we know that

we have a exponential function of the form

`f(x)=a(b^x)`

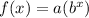
where

f(x) -----> the length of a snake in a video game in centimeters

x ----> the time in minutes

a is the initial value or y-intercept of the linear equation

b is the base of the exponential equation

In this problem

`f(x)=10(2^x)`

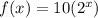
so

`a=10\ cm` ---> initial value, value of y when the value of x is equal to zero
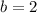`b=2` ----> factor growth

`b=(1+r)\\r=b-1=2-1=1`

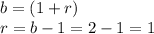
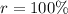`r=100\%` ----> percent rate of change

Is a exponential growth function

Part b) Graph the function

To graph the function we need different points

assume different values of x and find the values of f(x)

For x=0 ---->
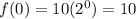`f(0)=10(2^0)=10` ----> point (0,10)

For x=1 ---->
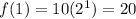`f(1)=10(2^1)=20` ----> point (1,20)

For x=2 ---->
`f(2)=10(2^2)=40` ----> point (2,40)

For x=3 ---->
`f(3)=10(2^3)=80` ----> point (3,80)

For x=4 ----> f(4)=10(2^4)=160 ----> point (4,160)

Plot the points, connect them and draw the graph

see the attached figure