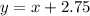Question

Please help me figure out

Answer 1

The equation of line will be
`y=x+2.75`

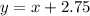
Explanation:

Given admission and
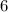`6` sample costs $
`8.75`

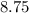
And admission and
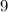`9` samples costs $
`11.75`

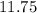
Let cost of the sample is
`y` and number of sample is
`x`

Now, we will find the slope of line

`m=(y_2-y_1)/(x_2-x_1)\\\\m=(11.75-8.75)/(9-6)\\\\m=(3)/(3)\\\\m=1`

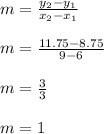
Plug slope as
`1` and point
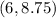`(6,8.75)` in the equation we get,

`(y-y_1)=m(x-x_1)\\y-8.75=1(x-6)\\y-8.75=x-6\\y=x-6+8.75\\y=x+2.75`

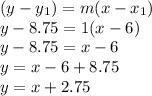
The equation of line will be
`y=x+2.75`