Question

Three roots of the polynomial equation X^4-4X^3-2X^2 +12 X +9=0 are 3, -1 and -1. Explain why the fourth root must be a real number. Find the fourth root

Answer 1

The fourth root is 3

If the 4th root is not a real therefore it must be a complex number (a+ib),and its conjugate will be also a root ,therefore there would be 5 roots instead of 4 roots.

Therefore the fourth root is real.

The roots are -1 with multiplicity 2 and 3 with multiplicity 2

Therefore it has four roots

Explanation:

Given polynomial equation is
`X^4-4X^3-2X^2+12X+9=0`

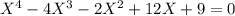
And also given that 3,-1 and -1 are the roots of the given polynomial equation

To find the fourth root of the polynomial equation and to solve the fourth root is real :

By synthetic division

_3| 1 -4 -2 12 9

0 3 -3 -15 -9

___________________

_-1| 1 -1 -5 -3 0

0 -1 2 3

___________________

1 -2 -3 0

Therefore x-3 and x+1 is a factor

Therefore 3 and -1 are roots

Now we have the quadratic equation
`x^2-2x-3=0`

`(x+1)(x-3)=0`

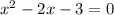
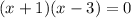
Therefore x=-1,3 are the roots

Therefore the fourth root is 3

If the 4th root is not a real therefore it must be a complex number (a+ib),and its conjugate will be also a root ,therefore there would be 5 roots instead of 4 roots.

Therefore the fourth root is real.

The roots are -1 with multiplicity 2 and 3 with multiplicity 2

Therefore it has four roots.