Question

consider the following quadratic function f(x)= -2x^2+12x+32=0 select all the statements that are true for the function

Answer 1

Answer: C- The value of the discrimination is 400.

E- The function has 2 real solutions.

Step-by-step explanation: Hope that helped!

Answer 2

The answer to your question is

a) 400

b) The function has two real solutions (-2 and 8)

Explanation:

Process

1.- Discriminant = b² - 4ac

= 12² -4(-2)(32)

= 144 + 256

= 400

2.- Solutions (using the general formula)

x =
`\frac{- b +/- \sqrt{b^(2)- 4ac}}{2a}`

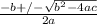
x =
`(- 12 +/- √(400))/(2(-2))`

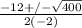
x =
`(-12 +/- 20)/(2(-2))`

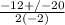
x₁ =
`(-12 + 20)/(2(-2)) = (-12 + 20)/(-4) = (-8)/(4) = - 2`

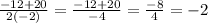
x₂ =
`(- 12 - 20)/(- 4) = (-32)/(- 4) = 8`

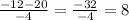
This function has two real solutions (-2, 8)