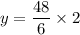Question

If y varíes directly as x, and y es 48 when x is 6? Which expression can be used to find the value of y when x is 2? Pleaseeee!!

Answer 1

Therefore the expression for y when x is 2 is

`y=(48)/(6)* 2`

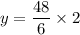
Explanation:

Given:

y varies directly as x, and y is 48 when x is 6

Means Direct Variation.

Therefore,

`y=kx`

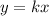
Where,

k = Constant of Proportionality

To Find:

y when x = 2

Solution:

First step we need to Find Constant of Proportionality

So put y = 48 and x = 6

Substituting the values we get

`48=k* 6\\\\k=(48)/(6)`

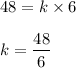
Now When x = 2 and
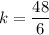`k=(48)/(6)` y will be

`y=(48)/(6)* 2`

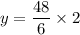
Therefore the expression for y when x is 2 is

`y=(48)/(6)* 2`