Question

Let u = (1,2), v = (−3,4), and w = (5,0)

a) Draw these vectors in ℝ2 .

b) Find scalars λ1 and λ2 such that w = λ1u + λ2v.

Answer 1

w-2u-v

Explanation:

Given are three vectors u, v and w.

In R^2 we treat first element as x coordinate and 2nd element as y coordinate.

Thus we mark (1,2) in the I quadrant, (-3,4) in II quadrant and (5,0) on positive x axis 5 units form the origin.

b)
`w=au+bv`

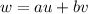
We have to find the values of a and b

`(5,0) = a(1,2)+b(-3,4)`]

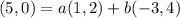Equate the corresponding terms

`5=a-3b\\0=2a+4b`

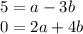
Divide II equation by 2 to get

`0=a+2b`

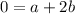
Eliminate a

-5 = 5b: b=-1

a=-2

Hence

w = 2u-v