Question

A 0.600 kg block is attached to a spring with spring constant 15 N/m. While the block is sitting at rest, a student hits it with a hammer and almost instantaneously gives it a speed of 44 cm/s.

What is the amplitude of the subsequent oscillations? Answer should be in cm.
What is the block's speed at the point where x= 0.70 A? Answer should be in cm/s.

Answer 1

8.8 cm

31.422 cm/s

Step-by-step explanation:

m = Mass of block = 0.6 kg

k = Spring constant = 15 N/m

x = Compression of spring

v = Velocity of block

A = Amplitude

As the energy of the system is conserved we have

`(1)/(2)mv^2=(1)/(2)kA^2\\\Rightarrow A=\sqrt{(mv^2)/(k)}\\\Rightarrow A=\sqrt{(0.6* 0.44^2)/(15)}\\\Rightarrow A=0.088\ m\\\Rightarrow A=8.8\ cm`

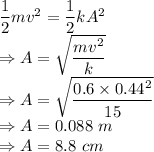
Amplitude of the oscillations is 8.8 cm

At x = 0.7 A

Again, as the energy of the system is conserved we have

`(1)/(2)kA^2=(1)/(2)mv^2+(1)/(2)kx^2\\\Rightarrow v=\sqrt{(k(A^2-x^2))/(m)}\\\Rightarrow v=\sqrt{(15(0.088^2-(0.7* 0.088)^2))/(0.6)}\\\Rightarrow v=0.31422\ m/s`

The block's speed is 31.422 cm/s