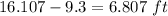Question

The diagram shows the outline of a room. The owner has decided to make the room three times as large as it is now. How many feet wide will the new room be?

Answer 1

New width will be
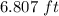`6.807\ ft` larger than old width.

Explanation:

Given width of room is
`9.3\ ft`

And length of room is
`6.2\ ft`

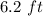
Then the old area will be
`(9.3* 6.2)`

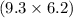
Also we have to make this room three times larger as it is now.

We can see the ratio between width and length of room is
`(9.3)/(6.2)=1.5`

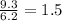
let us say the length of new room is
`x`

So, width of room will be
`1.5* x`

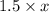
And we know area of rectangle is
`length* width`

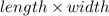
Also, the new area will be
`3* (9.3* 6.2)`

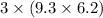
Then the equation will be

`x* 1.5* x=3*(9.3* 6.2)\\1.5* x^2=172.89\\x^2=(172.89)/(1.5)\\ x^2=115.32\\x=√(115.32)\\x=10.73\ ft`

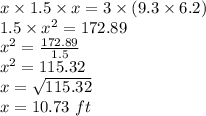
So, the width of new room is

`1.5* x=1.5* 10.738\\width=16.107\ ft`

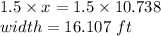
So, the increment in width is

`16.107-9.3=6.807\ ft`