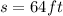Answer: 64 ft
Explanation:
We are given the following equation that models the baseball's parabolic path:
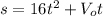 (1)
(1)
Where:
 is the ball maximum height
is the ball maximum height
 is the time
is the time
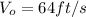 is the initial height
is the initial height
With this information the equation is rewritten as:
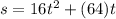 (2)
(2)
Now, we have to find
 , and this will be posible with the following formula:
, and this will be posible with the following formula:
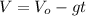 (3)
(3)
Where:
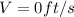 is the final velocity of the ball at the point where its height is the maximum
is the final velocity of the ball at the point where its height is the maximum
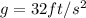 is the acceleration due gravity
is the acceleration due gravity
Isolating
 :
:
 (4)
(4)
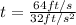 (5)
(5)
 (6)
(6)
Substituting (6) in (2):
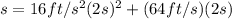 (7)
(7)
Finally: