Answer:
Option | and Option || is True
Explanation:
Given:
If the square root of
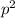 is an integer greater than 1,
is an integer greater than 1,
Lets p = 2, 3, 4, 5, 6, 7..........
Solution:
Now we check all option for
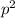
Option |.
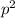 has an odd number of positive factors.
has an odd number of positive factors.
Let
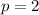
The positive factor of
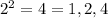
Number of factor is 3
Let
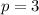
The positive factor of
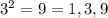
Number of factor is 3
So,
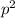 has an odd number of positive factors.
has an odd number of positive factors.
Therefore, 1st option is true.
Option ||.
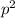 can be expressed as the product of an even number of positive prime factors
can be expressed as the product of an even number of positive prime factors
Let
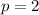
The positive factor of
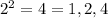

Let
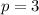
The positive factor of
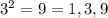
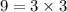
So, it is expressed as the product of an even number of positive prime factors,
Therefore, 2nd option is true.
Option |||.
p has an even number of positive factors
Let
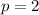
Positive factor of
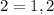
Number of factor is 2.
Let
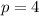
Positive factor of
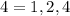
Number of factor is 3 that is odd
So, p has also odd number of positive factor.
Therefore, it is false.
Therefore, Option | and Option || is True.
Option ||| is false.