Question

Find the quotient. 22x2y2 ÷ 11x2y2

Answer 1

The guy up top is right its 2 with no mistake.

Explanation:

Answer 2

Quotient = 2

Solution:

Given expression is
`22x^2y^2/11x^2y^2`.

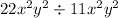To find the quotient.

`22x^2y^2/11x^2y^2=(22x^2y^2)/(11x^2y^2)`

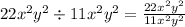
In numerator 22 can be written as 2 × 11.

`(22x^2y^2)/(11x^2y^2)=(2*11x^2y^2)/(11x^2y^2)`

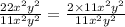
Take common term out in the numerator and denominator.

`(22x^2y^2)/(11x^2y^2)=((11x^2y^2)(2))/(11x^2y^2)`

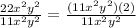
Common terms in the numerator and denominator will be cancelled.

`(22x^2y^2)/(11x^2y^2)=2`

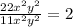
Hence the quotient is 2.