Question

Two carts are colliding on an airtrack (neglect friction). The first cart has a mass of m1=40 g and an initial velocity of v1=2 m/s. The second cart has a mass of m2=47 g and an initial velocity of v2=-5 m/s. Two experiments are conducted. In the first experiment, the first cart has a final velocity of v1'=-1.11 m/s.

What is the velocity of the second cart?

For the second experiment, the bumpers of the carts are modified, but the carts are started with the same initial velocities as before. Now the first cart has a final velocity of v1'=-3.8942 m/s, and the second cart a final velocity of v2'=0.0163 m/s.
How much (if any) energy was lost in the collision?

In good approximation, what kind of collision was the second experiment?

Answer 1

v₂ = -2.35m/s

This is an Inelastic collision

Step-by-step explanation:

Law of conservation of momentum

This states that for a collision occurring between two object in an isolated system, the total momentum of the two objects before the collision is equal to the total momentum of the two objects after the collision. That is, the momentum lost by object 1 is equal to the momentum gained by object 2.

Given from the question

m₁=40 g

initial velocity of m₁: v₁=2 m/s

m₂=47 g

initial velocity of m₂: v₂ = -5 m/s

final velocity of m₁: v'₁ = -1.11 m/s.

final velocity of m₂ = ?

second experiment final velocity of m₁ : v₁' = -3.8942 m/s

second experiment final velocity of m₂ : v₂' = 0.0163 m/s

Considering the first experiment

Apply the knowledge of conservation of momentum

`m₁v₁ + m₂v₂ =m₁v₁ + m₂v₂`

`(0.040)(2) + (0.047)(-5) = (0.040)(-1.11) + (0.040)v₂`

`v₂ = -2.35m/s`

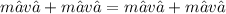
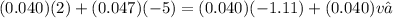
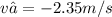
Considering the second experiment

initial kinetic energy
`KEₓ  = (1/2)m₁v₁² + (1/2)m₂v₂²`

`KEₓ = (1/2)(0.040)(2)² + (1/2)(0.047)(-5)²`

`KEₓ = 0.6675 J`

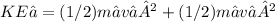
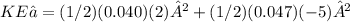
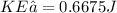
Final kinetic energy
`KEₙ = (1/2)m₁v₁² + (1/2)m₂v₂²`

`KEₙ = (1/2) (0.040) (-3.8942)² + (1/2) (0.047) (0.0163)²`

`KEₙ = 0.3033 J`

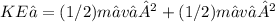
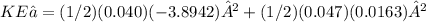
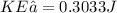
Loss in kinetic energy
`ΔKE = KEₓ - KEₙ`

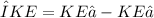
ΔKE = 0.6675 - 0.3033

ΔKE = 0.3642 J

This collision is a perfectly inelastic collision because the maximum kinetic energy is lost this means that the kinetic energy before the collision is not the same as the kinetic energy after the collision.Though momentum is conserved kinetic energy is not conserved.