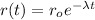Answer:
a)
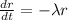
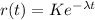
b)
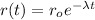
Explanation:
For this case we have the following info provided:
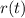 represent the amount of particular radioactive isotope at time t
represent the amount of particular radioactive isotope at time t
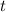 represent the time
represent the time
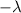 represent the decay rate parameter.
represent the decay rate parameter.
Part a
We can use the following proportional model given by this differential equation:
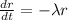
If we reorder the expression we got:
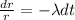
If we integrate both sides we got:
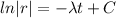
And if we apply exponentials we got:
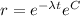
So then if
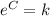 we can rewrite the model like this:
we can rewrite the model like this:
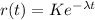
Part b
For this case since we know that
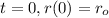 if we replace this condition in our formula we got:
if we replace this condition in our formula we got:
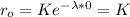
So then
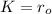 and our model is given by:
and our model is given by: