Question

Determine the upper limit of a 95% confidence level estimate of the population proportion when the sample size is 200 customers, 35 of whom respond yes to a survey.

Answer 1

Answer: 0.228

Explanation:

We know that the formula to find the upper limit of confidence interval for population proportion is given by :-

`\hat{p}+ z*\sqrt{\frac{\hat{p}(1-\hat{p})}{n}}` , where

n= Sample size

`\hat{p}` = Sample proportion

z* = critical value.

Let p be the proportion of customers who responds yes to a survey.

As per given , we have

n= 200

`\hat{p}=(35)/(200)=0.175`

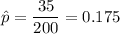
Confidence level : 95%

The critical z-value for 95% confidence is z* = 1.96 [ from z-table]

Substitute all values in the formula , we get

`0.175+(1.96)\sqrt{(0.175(1-0.175))/(200)}`

`=0.175+(1.96)√(0.000721875)`

`=0.175+(1.96)(0.0268677315753)`

`=0.227660753888\approx0.228`

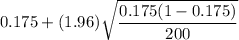
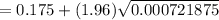
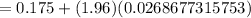
Hence, the upper limit of a 95% confidence level estimate of the population proportion is 0.228.