Question

Given the points A(0,0) B(6,3) and C(1.5,0.75) find the ratio that point C partitioned segment AB.

Answer 1

The ratio of AC to CB is 1.677 to 5.03

Explanation:

Step 1: Finding the distance of AC

By using distance formula

`AC = √((x_2 -x_1)^2 + (y_2 -y_1)^2)`

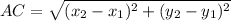
Substituting the values

`AC = √((1.5 -0)^2 + (0.75 -0)^2)`

`AC = √((1.5 )^2 + (0.75)^2)`

`AC = √(2.25 +0.5625 )`

`AC = √(2.8125 )`

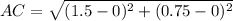
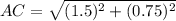
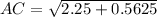
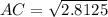
AC= 1.677

Step 2: Finding the distance of CB

`CB = √((6 - 1.5)^2 + (3 - 0.75)^2)`

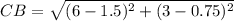
Substituting the values

`CB = √((4.5)^2 + (2.25)^2)`

`CB = √((20.25) + (5.0625))`

`CB = √(25.3125)`

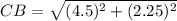
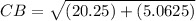
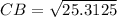
CB = 5.03

The Ratio is 1.677 to 5.03