Answer:
for an infinite geometric series the formula for the sum of the infinite geometric series when the common ratio is less than one is given by
 =
=
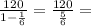
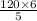 = 144.
= 144.
Explanation:
i) from the given series we can see that the first term is
 = 120.
= 120.
ii) let the common ratio be r.
iii) the second term is 20 = 120 × r
therefore r = 20 ÷ 120 =

iv) the third term is
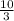 = 20 × r
= 20 × r
therefore r =
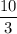 ÷ 20 =
÷ 20 =

v) for an infinite geometric series the formula for the sum of the infinite geometric series when the common ratio is less than one is given by
 =
=
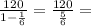
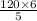 = 144.
= 144.