Question

Two chargedparticles, with charges q1=q and q2=4q, are located at a distance d= 2.00cm apart on the x axis. A third charged particle,with charge q3=q, is placed on the x axis such that the magnitude of the force that charge 1 exerts on charge 3 is equal to the force that charge 2 exerts on charge 3. ~Find theposition of charge 3 when q = 2.00 nC . ~ Assuming charge 1 is located at the origin of the x axisand the positive x axis points to the right, find the two possible values x3,r and x3,l for the position of charge 3. I am stuck on this conversion x^2=2(2-x)^2 to find the value for x!

Answer 1

Two possible points

x= 0.67 cm to the right of q1

x= 2 cm to the left of q1

Step-by-step explanation:

Electrostatic Forces

If two point charges q1 and q2 are at a distance d, there is an electrostatic force between them with magnitude

`\displaystyle f=k(q_1\ q_2)/(d^2)`

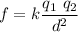
We need to place a charge q3 someplace between q1 and q2 so the net force on it is zero, thus the force from 1 to 3 (F13) equals to the force from 2 to 3 (F23). The charge q3 is assumed to be placed at a distance x to the right of q1, and (2 cm - x) to the left of q2. Let's compute both forces recalling that q1=1, q2=4q and q3=q.

`\displaystyle F_(13)=k(q_1\ q_3)/(d_(13)^2)`

`\displaystyle F_(13)=k((q)\ (q))/(x^2)`

`\displaystyle F_(23)=k(q_2\ q_3)/(d_(23)^2)`

`\displaystyle F_(23)=k((q)(4q))/((0.02-x)^2)`

`\displaystyle F_(23)=(4k\ q^2)/((0.02-x)^2)`

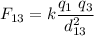
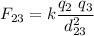
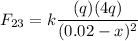
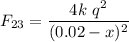
Equating

`\displaystyle F_(13)=F_(23)`

`\displaystyle (K\ q^2)/(x^2)=(4K\ q^2)/((0.02-x)^2)`

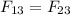
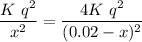
Operating and simplifying

`\displaystyle (0.02-x)^2=4x^2`

To solve for x, we must take square roots in boths sides of the equation. It's very important to recall the square root has two possible signs, because it will lead us to 2 possible answer to the problem.

`\displaystyle 0.02-x=\pm 2x`

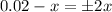
Assuming the positive sign :

`\displaystyle 0.02-x= 2x`

`\displaystyle 3x=0.02`

`\displaystyle x=0.00667\ m`

`x=0.67\ cm`

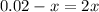
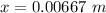
Since x is positive, the charge q3 has zero net force between charges q1 and q2. Now, we set the square root as negative

`\displaystyle 0.02-x=-2x`

`\displaystyle x=-0.02\ m`

`\displaystyle x=-2\ cm`

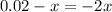
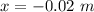
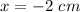
The negative sign of x means q3 is located to the left of q1 (assumed in the origin).