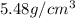To develop this problem we will apply the relationship of density, such as the unit of mass per unit volume of a body. For this relationship we will use the known constants of the value of the land's mass and its respective radius. These values will be converted from kilograms to grams and meters to centimeters respectively. We will find the volume through the geometric relationship of the sphere using the radius of the earth.
The mass of the Earth is given as
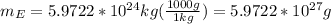
The radius of the Earth is
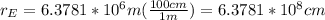
Using the geometric value of volume for a sphere, and using the radius of the earth, as the radius of that sphere we have to
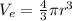
Replacing,
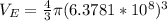
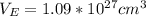
The expression for the density of the Earth is
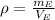
Replacing,
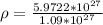
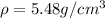
Therefore the average density of the earth is