Answer:
- Second-order nonlinear ordinary differential equation.
- Second-order linear ordinary differential equation.
- Third-order linear ordinary differential equation.
- Second-order nonlinear ordinary differential equation
Explanation:
The objective is to determine whether or not each of the following equation is linear:
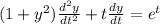
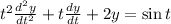
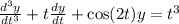

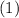
We can rewrite this equation in the form
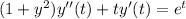 .
.
As we can see, this is an second-order nonlinear differential equation, because of the term
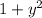 next to
next to
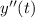 .
.
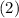
We can rewrite this equation in the form
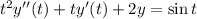 .
.
This is an second-order linear ordinary differential equation.
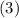
We can rewrite this equation in the form
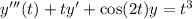
This is an third-order linear ordinary differential equation.
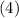
This is an second-order nonlinear ordinary differential equation, because of the term
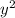 .
.