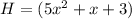Question

The area of a triangle is 15x^4+3x^3+4x^2-x-3 square meters. The length of the base of the triangle is 6x^2-2 meters. What is the height of the triangle?

Answer 1

The height of the triangle is:
`H = (5x^2 + x +3)`

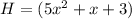
Explanation:

Here, the area the triangle is given as:
`15x^4 + 3x^3 + 4x^2 - x - 3`

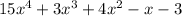
Also, base of the triangle =
`(6x^2 -2)`

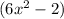
Let us assume the height of the triangle = H units

Now, AREA of TRIANGLE =
`(1)/(2) * B * H`

`\implies (15x^4+3x^3+4x^2-x-3 ) = (1)/(2) * ( 6x^2-2) * H\\\implies H =( (15x^4+3x^3+4x^2-x-3 ))/((3x^2-1))`

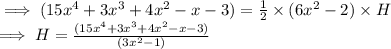
Solving by LONG DIVISION, we get:

`H = (5x^2 + x +3)`

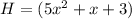
Hence, the height of the triangle is:
`H = (5x^2 + x +3)`