Question

If x2 + y2 = 25, what is the value of

at the point (4,3)?
O A. -25/27
OB.-7/27
OC. 7/27
D. 3/4
OE. 25/27

Answer 1

A. -25/27

Explanation:

Given:

The equation is given as:

`x^2+y^2=25`

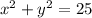
To find:
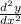`(d^2 y)/(dx^2)` at (4, 3)

Differentiating the above equation with respect to 'x', we get:

`(d)/(dx)(x^2+y^2)=(d)/(dx)(25)\\\\2x+2yy'=0\\\\x+yy'=0\\\\yy'=-x\\\\y'=(-x)/(y)------- (1)`

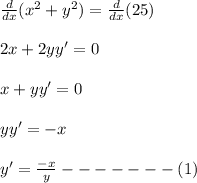
Value of
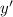`y'` at (4,3) is given as:

`y'_((4,3))=-(4)/(3)-------- (2)`

Now, differentiating equation (1) with respect to 'x' again, we get:

`y''=(d)/(dx)((-x)/(y))\\\\y''=(y(-1)-(-x)y')/(y^2)\\\\y''=(-y+xy')/(y^2)`

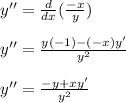
Now, value of
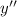`y''` at (4,3) is given as by plugging 4 for 'x', 3 for 'y' and
`(-4)/(3)` for
`y'`

`y''_((4,3))=(-3+(4)(-(4)/(3)))/(3^2)\\\\y''_((4,3))=(-3-(16)/(3))/(9)\\\\y''_((4,3))=(-9-16)/(3)/ 9\\\\y''_((4,3))=(-25)/(3)/ 9\\\\y''_((4,3))=(-25)/(3)* (1)/(9)\\\\y''_((4,3))=-(25)/(27)`

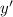
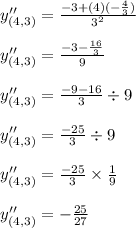
Therefore, the value of the second derivative at (4, 3) is option (A) which is equal to -25/27.