Question

For each random variable, state whether the random variable should be modeled with a Binomial distribution or a Poisson distribution. Explain your reasoning. State the parameter values that describe the distribution and give the probability mass function.

Random Variable 1. A quality measurement for cabinet manufacturers is whether a drawer slides open and shut easily. Historically, 2% of drawers fail the easy slide test. A manufacturer samples 10 drawers from a batch. Assuming the chance of failure is independent between drawers, what type of distribution could be used to model the number of failed drawers from the sample of 10?

Random Variable 2. The warranty for a particular system on a new car is 2 years. During which there is no limit to the number of warranty claims per car. Historically, the average number of claims per car during the period is 0.8 claims. What type of distribution could be used to model the number of warranty claims per car?

Answer 1

1) This random variable should be modelled using a binomial distribution since we have independence between the events and a bernoulli trial each time when the experiment is conducted, a fixd value for the sample size n and for the probability of success.

Let X the random variable of interest, on this case th distribution would be given by:

`X \sim Binom(n=10, p=0.02)`

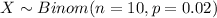
The probability mass function for the Binomial distribution is given as:

`P(X)=(nCx)(p)^x (1-p)^(n-x) = (10Cx) (0.02)^x (1-0.02)^(10-x)`

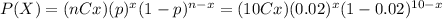
2) For this case we don't have a sample size provided and we just have an average rate for a given period, so then we can assume that the best distribution for this case is the Poisson distribution.

Let X the random variable that represent the number of claims per car. We know that
`X \sim Poisson(\lambda)`

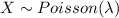
The probability mass function for the random variable is given by:

`f(x)=(e^(-\lambda) \lambda^x)/(x!) , x=0,1,2,3,4,...`

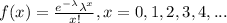
Where
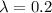`\lambda=0.2` represent the mean of occurrences in the interval of 2 years provided.

And f(x)=0 for other case.

Explanation:

Previous concepts

The binomial distribution is a "DISCRETE probability distribution that summarizes the probability that a value will take one of two independent values under a given set of parameters. The assumptions for the binomial distribution are that there is only one outcome for each trial, each trial has the same probability of success, and each trial is mutually exclusive, or independent of each other".

Random variable 1

This random variable should be modelled using a binomial distribution since we have independence between the events and a bernoulli trial each time when the experiment is conducted, a fixd value for the sample size n and for the probability of success.

Let X the random variable "number of failed drawers", on this case th distribution would be given by:

`X \sim Binom(n=10, p=0.02)`

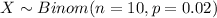
The probability mass function for the Binomial distribution is given as:

`P(X)=(nCx)(p)^x (1-p)^(n-x) = (10Cx) (0.02)^x (1-0.02)^(10-x)`

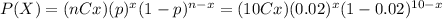
Where (nCx) means combinatory and it's given by this formula:

`nCx=(n!)/((n-x)! x!)`

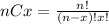
Random variable 2

For this case we don't have a sample size provided and we just have an average rate for a given period, so then we can assume that the best distribution for this case is the Poisson distribution.

Let X the random variable that represent the number of claims per car. We know that
`X \sim Poisson(\lambda)`

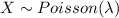
The probability mass function for the random variable is given by:

`f(x)=(e^(-\lambda) \lambda^x)/(x!) , x=0,1,2,3,4,...`

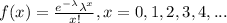
Where
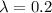`\lambda=0.2` represent the mean of occurrences in the interval of 2 years provided.

And f(x)=0 for other case.