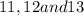Question

Five times the smallest of three consecutive integers is 17 less than twice the sum of the integers. Find the integers

Answer 1

The integers are 11,12 and 13

Explanation:

Let x,x+1,x+2 be the three consecutive integers. Let x be the smallest of three consecutive integers.

Then the expression can be written as

`5x=2(x+x+1+x+2)-17`

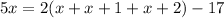
Adding the x terms, we get,

`5x=2(3x+3)-17`

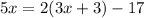
Multiply the term
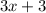`3x+3` by 2,

`5x=6x+6-17`

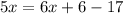
Adding the constant terms, we get,

`5x=6x-11`

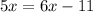
Subtracting 6x from both sides of the equation, we get,

`-x=-11`

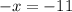
Thus,
`x=11`

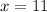
Substituting the value of x in x+1 and x+2, we get the value of three consecutive integers.

`x+1=11+1=12\\x+2=11+2=13`

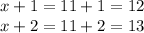
Thus, the three consecutive integers are
`11,12 and 13`

Answer 2

The integers are 11, 12, 13

Explanation:

Given:

Five times the smallest of three consecutive integers is 17 less than twice the sum of the integers

To Find:

The integers = ?

Solution:

Let the 3 consecutive integer be

n , n+1 , n+2

then

5 times the smallest of the integer. i

here the smallest integer is n

5n = 17 less than twice the sum of the integers

The sum of the integer is

=> n+n+1+n+2

Now

5n = 17 less than twice( n+n+1+n+2)

5n = 17 less than 2( n+n+1+n+2)

5n = 2( n+n+1+n+2) - 17

Solving the equation,

5n = 2( 3n +3) - 17

5n = 6n + 6 - 17

5n -6n = 6 - 17

-n = -11

n =11

Then

n+1 = 11+1 = 12

n+2 = 11+2 =13